티스토리 뷰
더 깔끔한 노션을 원한다면
세그먼트 트리(Segment Tree)
데이터를 효율적으로 저장하고, 빠른 시간에 탐색, 수정 및 추가 삭제 연산을 진행
www.notion.so
데이터를 효율적으로 저장하고, 빠른 시간에 탐색, 수정 및 추가 삭제 연산을 진행
구간 트리(Segment Tree)는 이 트리 구조의 이점을 살려서 특정 구간에서의 최대, 최소 값등을 빠르게 구할 수 있도록 합니다.
특히, 일차원 배열의 특정 구간에 대한 질문들(최대, 최소, 합 등)을 빠르게 구하는데 사용.
즉, 구간의 개수가 클 때 세그먼트 트리를 생각하자.
Segment Tree를 이용하여 특정 구간의 값(최대, 최소, 합 등)을 미리 전처리해서 부모 노드에 저장한다.
그로 인해 훨씬 더 빠른 시간에 탐색할 수 있다.
1. Segment Tree 배열의 크기는 4배로!
SegmentTree(int[] arr, int n) {
segmentArr = new int[n * 4];
Arrays.fill(segmentArr, Integer.MAX_VALUE);
init(arr, 0, n - 1, 1);
}입력 배열(numbers)의 크기보다 작지 않은 2^k의 k값을 구한다.
세그먼트 트리의 크기는 2^(k+1)이 되는데, 편리하게 n*4로 구현한다.
2. Segment 초기화는 재귀로!
static int init(int arr[], int left, int right, int node) {
if (left == right) {
return segmentArr[node] = arr[left];
}
int mid = (left+right)/2;
return segmentArr[node] = Math.min(init(arr, left, mid, node*2), init(arr, mid+1, right, node*2+1));
}init 함수는 (가장 초기상태의 트리)를 구하는 과정이다.
이 초기화 과정을 거치고 나면 결국 구간 최소 트리가 형성된다.
node 매개변수에 node2와 node2 + 1가 의미하는 것은 각 노드의 왼쪽 자식, 오른쪽 자식이다.
left와 right가 같다는 것은 구간의 크기가 1이라는 의미로 각 리프 노드로 자리잡는다.
만약 구간 합 트리를 구하고 싶으면 다음과 같은 코드를 사용하면 된다.
static int init(int arr[], int left, int right, int node) {
if (left == right) {
return segmentArr[node] = arr[left];
}
int mid = (left+right)/2;
return segmentArr[node] = init(arr, left, mid, node*2) + init(arr, mid+1, right, node*2+1);
}예를 들어 배열의 크기가 12인 arr이 있다고 가정하자.
arr = {75, 30, 100, 38, 50, 51, 52, 20, 81, 5, 39, 20};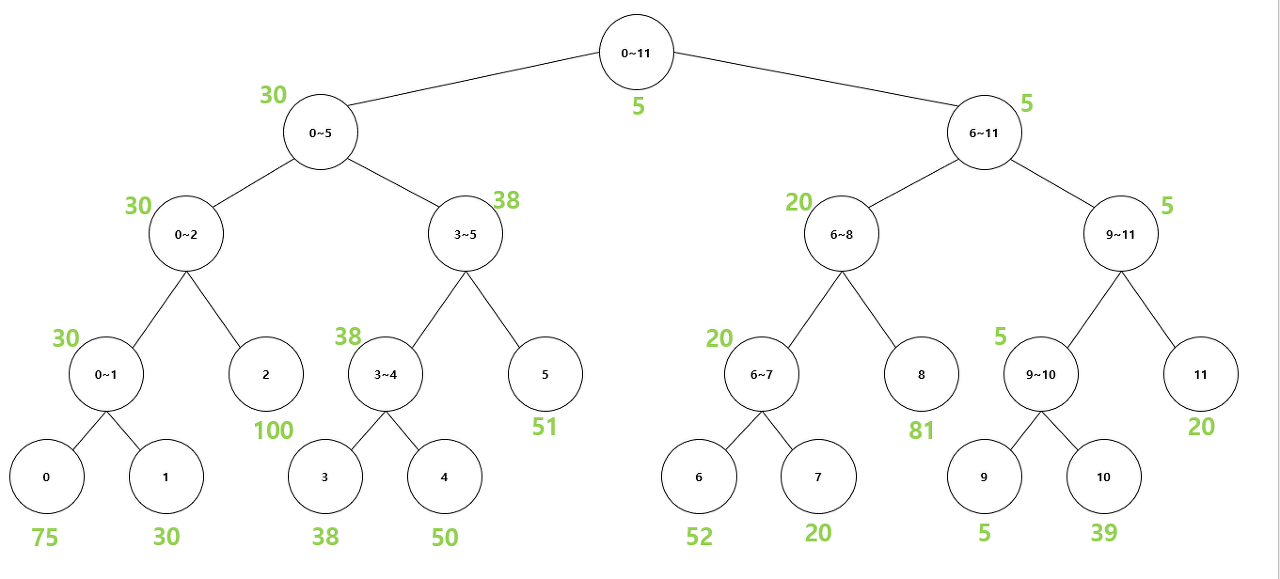
SegmentArr에는 다음 그림과 같이 값이 저장되게 된다.
3. 구간 최소 역시 재귀로!
static int query(int start, int end, int node, int nodeLeft, int nodeRight) {
if (start > nodeRight || end < nodeLeft){
return Integer.MAX_VALUE;
}
if (start <= nodeLeft && end >= nodeRight) {
return segmentArr[node];
}
int mid = (nodeLeft + nodeRight) / 2;
return Math.min(query(start, end, node * 2, nodeLeft, mid), query(start, end, node * 2 + 1, mid + 1, nodeRight));
}3-1. 구간을 벗어남
if (start > nodeRight || end < nodeLeft){
return Integer.MAX_VALUE;
}구간을 벗어났을 때에는 Integer.MAX_VALUE를 return하여 그 아래 구간까지 재귀가 못 미치게 한다.
3-2. 구간을 접함
if (start <= nodeLeft && end >= nodeRight) {
return segmentArr[node];
}구간에 접하게 되면 해당 노드를 return해준다.
3-3. 그 외에는 재귀로 탐색
return Math.min(query(start, end, node * 2, nodeLeft, mid),
query(start, end, node * 2 + 1, mid + 1, nodeRight)
);둘다 아닌 상황에는 재귀를 통해 해결한다.
init에서 했던 것과 비슷하게 node * 2와 node * 2 + 1인 node의 왼쪽, 오른쪽 자식에서 탐색해준다.
Example : 3~6 구간
/** 1. 초기값
* start : 3
* end : 6
* node : 1
* nodeLeft : 0
* nodeRight : 11
*/
Math.min(query(3, 6, 2, 0, 5), query(3, 6, 3, 6, 11));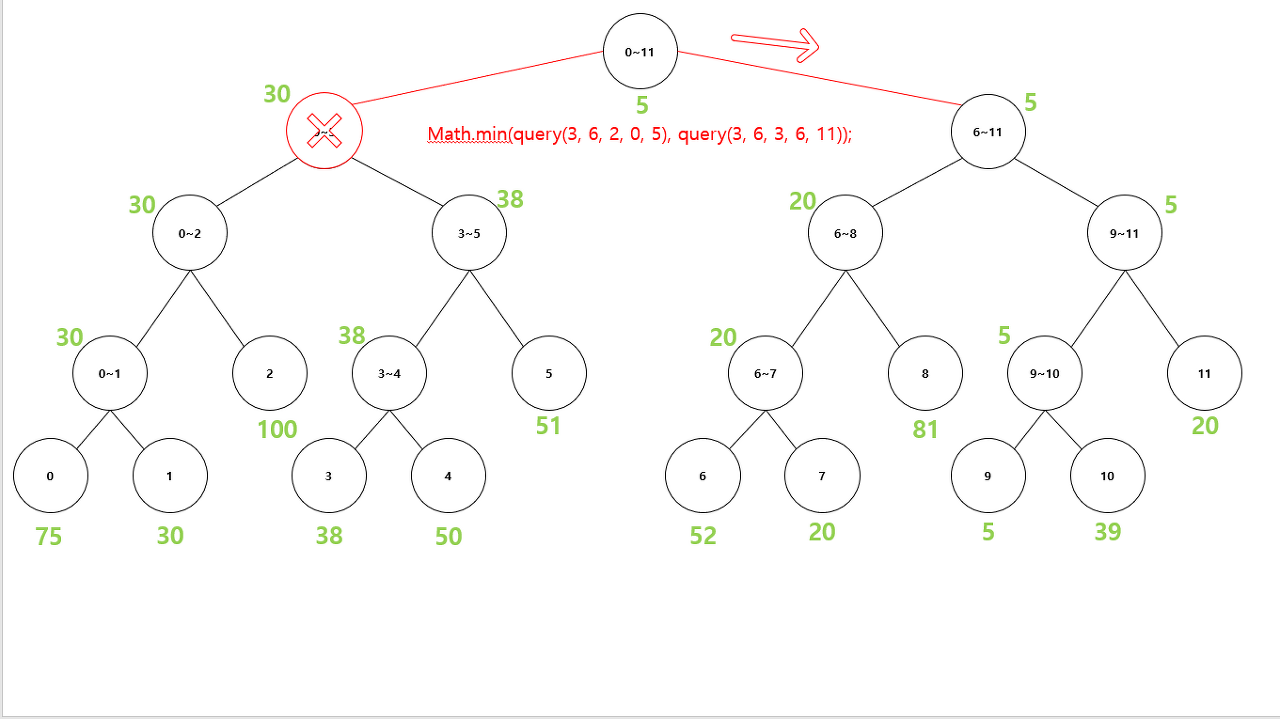
/** 2. 초기값
* start : 3
* end : 6
* node : 3
* nodeLeft : 6
* nodeRight : 11
*/
Math.min(query(3, 6, 6, 6, 8), query(3, 6, 7, 9, 11));오른쪽 자식노드의 값이 더 작지만 범위를 벗어났으므로 Integer.parseInt가 채워지게 된다.
그러므로 왼쪽 자식 노드의 값으로 내려가게 된다.
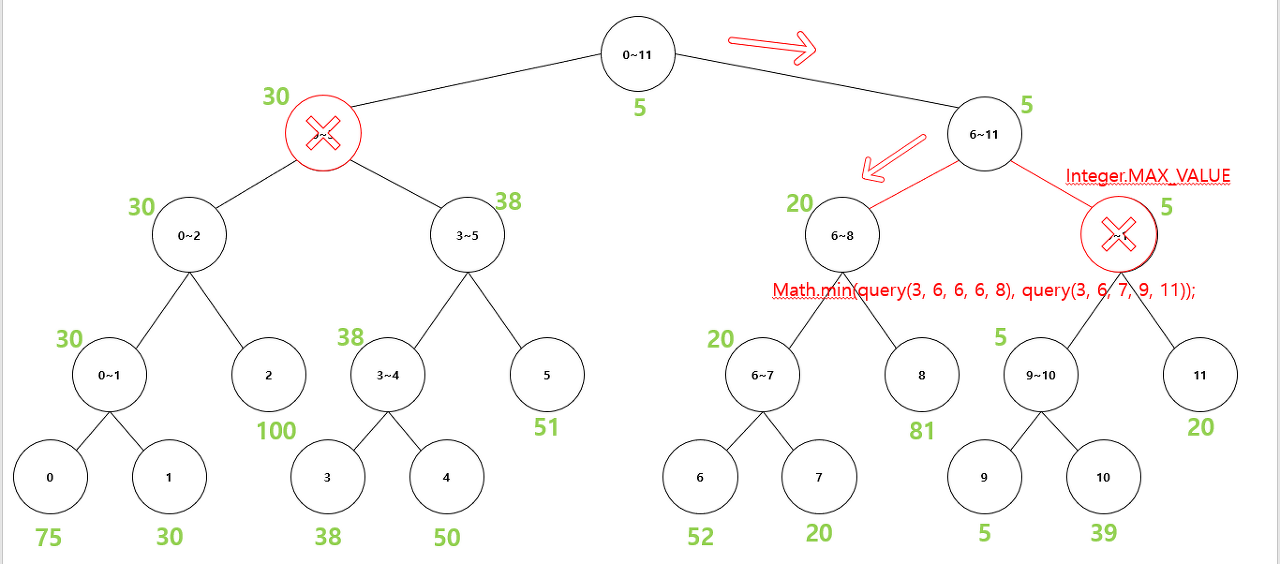
그러므로 최종적으로 20이 출력되게 된다.
결론
세그먼트 트리는 전처리를 통해 미리 구간의 쿼리를 정해놓아 빠르게 탐색할 수 있는 자료구조이다.
쿼리의 예로는 구간 최대, 최소, 합 등이 있다.
아래 문제를 풀어보면서 이해를 더해보자.
10868번: 최솟값
N(1 ≤ N ≤ 100,000)개의 정수들이 있을 때, a번째 정수부터 b번째 정수까지 중에서 제일 작은 정수를 찾는 것은 어려운 일이 아니다. 하지만 이와 같은 a, b의 쌍이 M(1 ≤ M ≤ 100,000)개 주어졌을 때는
www.acmicpc.net
2042번: 구간 합 구하기
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 합을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄��
www.acmicpc.net
2357번: 최솟값과 최댓값
N(1 ≤ N ≤ 100,000)개의 정수들이 있을 때, a번째 정수부터 b번째 정수까지 중에서 제일 작은 정수, 또는 제일 큰 정수를 찾는 것은 어려운 일이 아니다. 하지만 이와 같은 a, b의 쌍이 M(1 ≤ M ≤ 100
www.acmicpc.net
출처
세그먼트 트리(Segment Tree)
세그먼트 트리(Segment Tree)는 요청하는 쿼리에 대해 방식이 달라질 수 있으나, 모든 쿼리를 다룰 수 없기에 구간 합에 대한 세그먼트 트리를 정리해 두었습니다. 내용이 길지만 그만큼 자세히 설��
www.crocus.co.kr
'알고리즘' 카테고리의 다른 글
| Baekjoon 2042 구간 합 구하기 - 세그먼트 트리(구간 합, 수정) (0) | 2020.10.09 |
|---|---|
| Baekjoon 10868 최솟값 - 세그먼트 트리 (0) | 2020.10.09 |
| 풀어보면 좋은 문제 (0) | 2020.10.09 |
| Baekjoon 3111 검열 - 문자열+스택 (0) | 2020.10.04 |
| Baekjoon 2505 두 번 뒤집기 (0) | 2020.10.03 |
- Total
- Today
- Yesterday
- 이펙티브 자바
- 클린 코드
- 클린 아키텍처
- BAEKJOON
- Kotlin
- Olympiad
- Effective Java
- 프로그래머스
- 디자인 패턴
- MSA
- kotest
- JPA
- BOJ
- 테라폼
- 코테
- node.js
- 이팩티브 자바
- AWS
- 정규표현식
- 객체지향
- 알고리즘
- Java
- 디자인패턴
- Spring Boot
- 백준
- Algorithm
- C++
- programmers
- Spring
- kkoon9
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
